AlwaysLearn

A DFT and FFT TUTORIAL

A DFT is a "Discrete Fourier Transform". An FFT is a "Fast Fourier Transform". An FFT is a DFT, but is much faster for calculations. The whole point of the FFT is speed in calculating a DFT.

DFT and FFT

FFT

Constructing A 4 Input Butterfly Diagram

<< Previous Next >>

Here I will show you step-by-step how to construct a 4 input Butterfly Diagram.

 

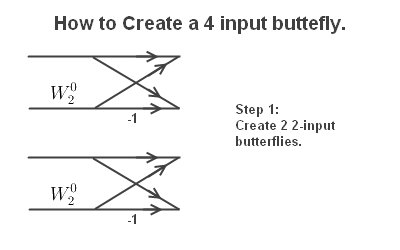
Create 4 Input Butterfly part 1

Next extend lines and connect upper and lower butterflies.

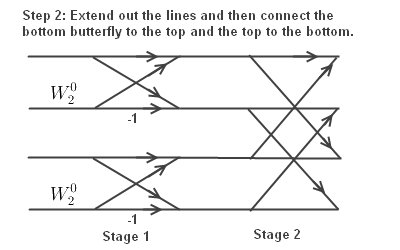
Create 4 Input Butterfly part 2

Finally, labeling the butterfly.

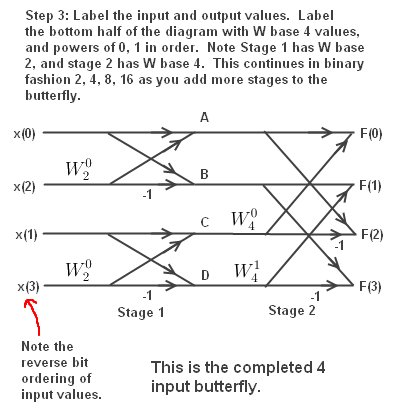
Creating a 4 input Butterfly part 3

Note the order of input values is "reverse bit" order. The Butterfly uses the natural expansion order of the Danielson-Lanczos Lemma, which is why the input is ordered that way. This was described earlier.

The four output equations for the butterfly are derived below.

Butterfly Derived Equations, 4 input

Equation 12

The N Log N savings

Remember, for a straight DFT you needed N*N multiplies. The N Log N savings comes from the fact that there are two multiplies per Butterfly. In the 4 input diagram above, there are 4 butterflies. so, there are a total of 4*2 = 8 multiplies. 4 Log(4) = 8. This is how you get the computational savings in the FFT! The log is base 2, as described earlier. See equation 1.

In the next part I provide an 8 input butterfly example for completeness.

<< Previous Next >>